Have you ever had an idea you couldn’t quite shake? Something that worms it’s way into your brain for one reason or another and just wont leave. Always on the backburner, thinking about it in the shower every day, in the bed as you go to sleep at night, zoning out in the living room, for as long as you can remember?

For me, that thing is the shape of data. Let me try to explain why:

Quickly grabbing a definition for “data”:

the quantities, characters, or symbols on which operations are performed by a computer, being stored and transmitted in the form of electrical signals and recorded on magnetic, optical, or mechanical recording media.

Now, consider that the definition of “data” you just read about IS data. It’s recursive, it’s enigmatic, it’s patterns, it’s noise, it’s signals, it’s encoded, it’s decoded, it’s referential, it’s turtles all the way down.

Before I lose you here with my emphatic excitement for the endless turmoil that is “data”, let’s zoom in on something more understandable to get our bearings. I’m going to talk about a common compression format (PKZip) for a bit because it touches on a lot of the topics that are relevant to the bigger picture.

How a ZIP File Format is Unpacked

When you try to open a .zip file on your computer a few things happen. There’s some calls behind the scenes that look at the file extension of example.zip and use your operating system (OS) to map it to a program that your computer has been told can open that file extension.

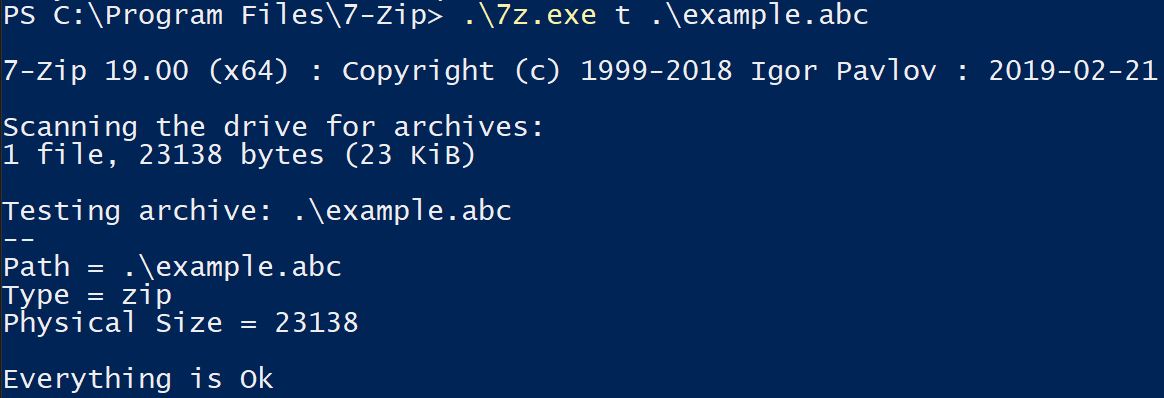
Your computer may have the popular “7-Zip” program assigned to handle .zip files, in which case a call will be made roughly as follows.

7z.exe x "example.zip"

The “x” argument tells 7-Zip that the contents of zip archive should be extracted. So 7-Zip reads the first few bytes of the file to check if certain magic numbers (also called magic bytes, file signatures, file headers, etc…) for the values 50 4B 03 04 are present. These values in text format are PK␃␄, AKA the bytes that identify the start of the PKZip (Zip) archive file format.

Then 7-Zip will go through and attempt to extract out relevant information and sections of the data, decompress sections of data that represent other files, as well as the attributes of those files such as the filenames and timestamps.

Finally, you get your extracted files from the .zip file.

There’s a lot more to the process, but for our purposes we’re just gonna ignore it for the time being.

• Source: ZIP archive file: format specification

Identify the guardrails

Now, let’s explicitly call out just a few of the things that were part of the above process that tried to make sure that your zip file opened correctly.

1. The file you were opening had the .zip file extension.

File extensions are completely arbitrary. Changing the extension to .abc does not modify the contents of the file itself, so if it was a PKZip file format before, it’s still a PKZip file format after.

In fact, many of the file extensions you see every single day are actually PKZip file formats. To name a few:

.apk (Android Apps)
.docx (Word Documents)
.epub (E-Books)
.ipa (iPhone Apps)
.jar (Java Apps)
.msix (Windows Apps)
.pptx (Powerpoint Files)
.xlsx (Excel Files)
.xpi (Firefox Browser Extensions)

You can even remove the file extension entirely and the file is still a valid PKZip file. A file extension simply exists to help map a file to a program that is most likely to be able to correctly parse it.

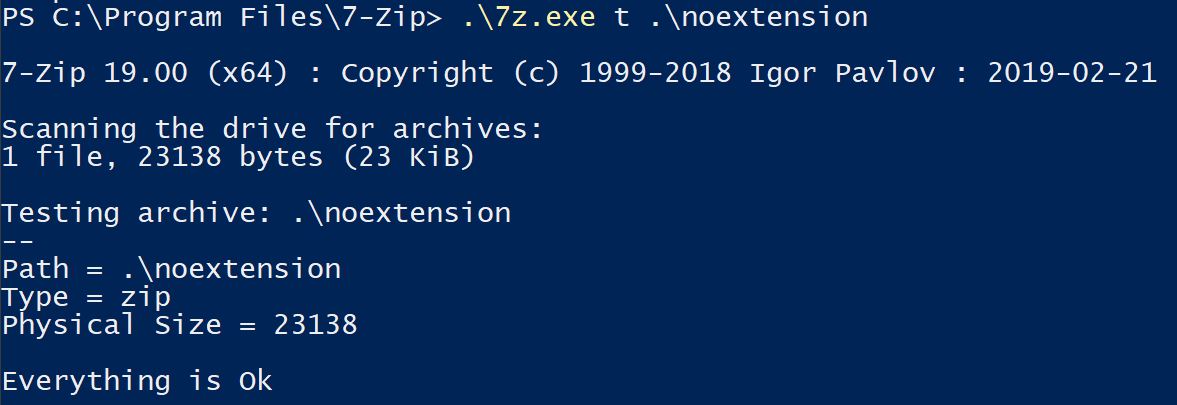
2. Your computer thought 7-Zip could open the file.

Branching off of the above point that file extensions are arbitrary, there’s no guarantee that a .zip file is actually the PKZip file format. There is no guarantee that the contents of the file aren’t just complete trash unrelated to the PKZip file format, so there is therefor no guarantee that the program 7-Zip can open a file with the .zip file extension.

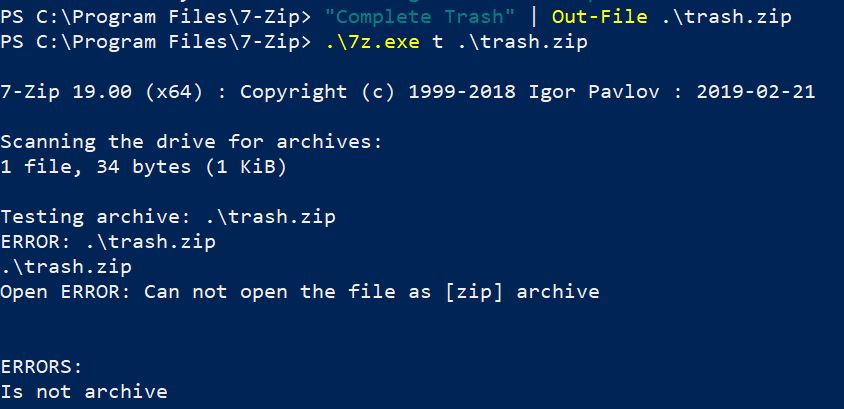
3. The magic numbers for a PKZip mean that it’s a PKZip file format

This is the first line item that actually deals with the contents of the file. If the bytes at the start of a file are 50 4B 03 04 then it matches the magic bytes for the PKZip file format. So let’s do exactly that, let’s put exactly those bytes in a file and see what happens.

00000000: 504b 0304                                PK..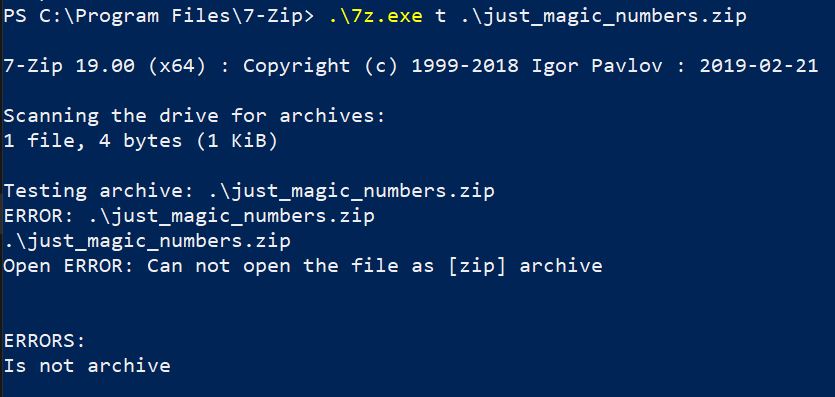

We still get an error because magic numbers in a file do not necessarily mean that a file is anything at all. They may be there entirely by chance!

For example, we know that the magic numbers 50 4B 03 04 are 4 bytes. Each byte position can have 1 of 256 different possible values. This means that if you generated 4 completely random bytes, there would be a 1 in 183,181,376 chance that it would end up being the same magic numbers as the PKZip’s magic numbers. I know that seems like a really small chance, but consider that you generate a bunch of reports every day and you stamp the report with a integer number at the start of the file. When you hit report #67,324,752, you end up with the magic number of the PKZip file format.

Python 3.9.3
>>> from struct import *
>>> #Pack integer 67324752 as int
>>> pack('i', 67324752)
b'PK\x03\x04'

Sure, I’ll concede the latter example is a stretch, but the point I’m trying to make is that it’s within the realm of possibilities.

Zooming Back Out

Above, I discussed a file format PKZip to highlight some of the ways systems are structured to make it probable that a file format was able to be correctly parsed as well as call out some attributes that are exposed to the end-user that aren’t always part of the actual data. File formats are data, but not all data are file formats.

• But why wouldn’t all data be a file format?

I mean file format in a traditional sense:

• A file containing data realted to a word document is a file format and data.
• A completely randomly generated set of 512 bytes for use in a cryptographic operation is not a file format, but it is still data.

We’ve come so far in computing and optimized day-to-day operations we’ve become accustomed to the hooks and helpers that differentiate the data from the file format.

There’s nothing wrong with a file opening as expected! But if you suspend all assumptions and expectations, I believe that you will find a thing of beauty. A whole world of mystery and chance hidden just below the surface.

This is the data I want to tell you about.

The Inherent Attributes of Data

Data has length:

• The length may be zero.
• The length may be determined.
• The length may be undetermined and approach infinity.

Data has values:

• The values may mean nothing (See: Length of zero)
• The values may mean something.

I hope this helped clarify some things 😋. Let’s dig in to the easiest one’s first with some examples.

The length may be zero in cases where, much like math, the concept of zero holds a place for nothing. If you save an empty text file on your computer, the data has nothing of value and zero length, but clearly still exists. It’s a tangible, real, thing you can double-click to open and reveal emptiness with no values or length.

The length may be undetermined and approach infinity in cases where the data is effectively an endless stream. A good example to really solidify this concept is Cosmic Microwave Background Radiation (CMBR). CMBR is an ever-present frequency that can be measured no matter where you are in the universe. The origin of this frequency is related the “Big Bang”. For all intents and purposes, it can be observed infinitely and definitely, definitely mean something.

Now we land on my favorite section of data:

• Data that has a deterministic length and may mean something.

The numbers mason, what do they mean?!?

Let’s take a look at this data, but by looking at it as little as possible. Actually, actively refuse to look at it directly unless absolutely necessary. No one knows what it means, but it’s provocative.

00000000: 0100 0000 0472 656d 7900 0100 0000 0472
00000010: 656d 7900 0100 0000 0472 656d 7900 0100
00000020: 0000 0472 656d 7900 0100 0000 0472 656d
00000030: 7900 0100 0000 0472 656d 7900 0100 0000
00000040: 0472 656d 7900 0100 0000 0472 656d 7900
00000050: 0100 0000 0472 656d 7900 0100 0000 0472
00000060: 656d 7900 0100 0000 0472 656d 7900 0100
00000070: 0000 0472 656d 7900 0100 0000 0472 656d
00000080: 7900 0100 0000 0472 656d 7900 0100 0000
00000090: 0472 656d 7900 0100 0000 0472 656d 7900
000000a0: 0100 0000 0472 656d 7900 0100 0000 0472
000000b0: 656d 7900 0100 0000 0472 656d 7900 0100
000000c0: 0000 0472 656d 7900 0100 0000 0472 656d
000000d0: 7900 0100 0000 0472 656d 7900 0100 0000
000000e0: 0472 656d 7900 0100 0000 0472 656d 7900

It has a defined length of 240 bytes. If you can read hex, you’ve probably already spotted some details, but let’s pretend that you can’t do that and refuse to look at the data from here on out okay?

How might you approach this block of 240 bytes of data?

First, let’s try to determine the entropy, or how random the data is by using an algorithm for calculating Shannon Entropy for which you can grab an implementation in almost any code language here.

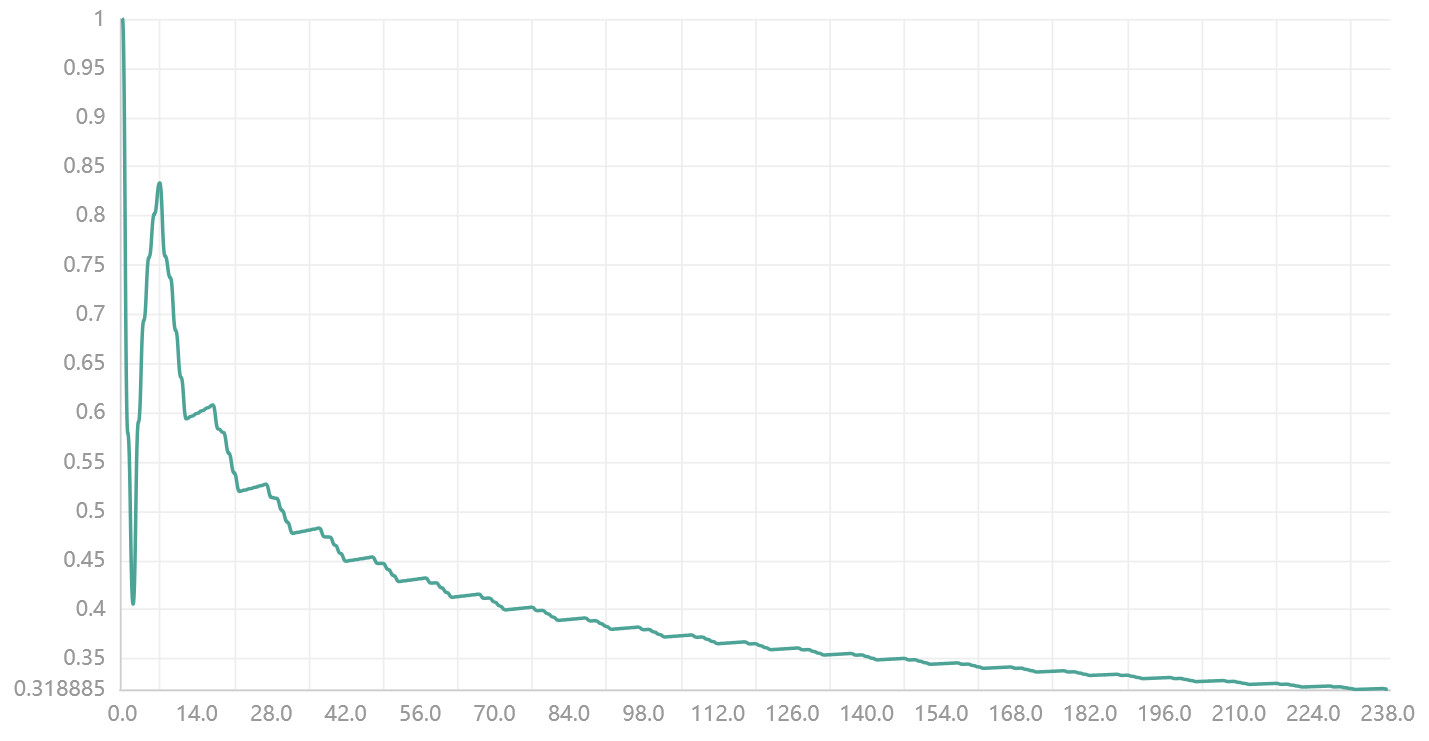
The X-Axis represents the position of the currently read data by the algorithm, while the Y-Axis represents how “random” the data is up until that position (Scaled from 0–>1).

Reading this graph we can see that initially the values are more random than the “nothing” that exists before the data starts (resulting in the initial spike), then steadily decreases as more values are read from the data.

This may indicate that the data isn’t very random, potentially even repetitive.

Another way we can approach this from a information theory perspective is by leveraging lossless data compression. An important attribute of most lossless data compression algorithms is that they cannot “lose” data when making a compressed archive, they can simply encode or represent the original data in an optimized “dense” format.

An easily understandable example is Run-length Encoding (RLE) for which repetitive data can be encoded in a much denser format.

A RLE compressed representation of a screen containing black and white pixels may be represented as:

12W1B12W3B24W1B14W where 12W1B(...) expands out to WWWWWWWWWWWWB(...)

Circling back to zip files, let’s create a Zip archive (lossless compression) of our example data which produces…

00000000: 504b 0304 1400 0000 0800 1ab4 3154 97ac  PK..........1T..
00000010: d521 0e00 0000 f000 0000 0b00 0000 7265  .!............re
00000020: 6d79 6861 782e 6269 6e63 6460 6060 294a  myhax.bincd```)J
00000030: cdad 6418 192c 0050 4b01 023f 0014 0000  ..d..,.PK..?....
00000040: 0008 001a b431 5497 acd5 210e 0000 00f0  .....1T...!.....
00000050: 0000 000b 0024 0000 0000 0000 0020 0000  .....$....... ..
00000060: 0000 0000 0072 656d 7968 6178 2e62 696e  .....remyhax.bin
00000070: 0a00 2000 0000 0000 0100 1800 1890 3512  .. ...........5.
00000080: 1c0c d801 b407 a3eb 1e0c d801 2de0 7891  ............-.x.
00000090: 1d0c d801 504b 0506 0000 0000 0100 0100  ....PK..........
000000a0: 5d00 0000 3700 0000 0000                 ]...7.....

The resulting Zip archive of our example data is only 170 bytes! And that’s including additional stuff like magic numers, timestamp, filename, etc…

This means that at minimum the lossless compression utility was able to encode 70 bytes of repetitive or patterned data in a more optimized format. This again, indicates that the data isn’t very random, potentially even repetitive.

To prove why this works, if I generate a 240 byte file with random values and try to compress it using the same utility it actually produces a Zip archive that is 402 bytes. The compressed random data is larger than the original, at least in part because it lacks any pattern to encode.

Identifiying Patterns and Repetition

Now that we know that there is likely to be patterns or repetition in our data, how might we approach finding them?

We can use something called frequency analysis. The core concept of which is knowing that each byte can be a value of 0–>255, so we simply count how many occurrences we see of that byte value. Putting this frequency analysis in graph format:

The X-Axis ranges from byte value 0–>255, while the Y-Axis represents how many times this value was seen in the data.

We see that the most common is 00 (Count 96), with the 6 others ranking equally (Count 24 Each). This may indicate to us that the 6 equally ranking values are part of the pattern, with 00 potentially being part of the pattern as well but occurring more frequently.

And so we finally have a theory as to the shape of the data:

• The data likely has a pattern within is that consumes most of the length.
• The pattern likely consists of predominantly 00.
• The pattern likely contains 01, 04, 72, 65, 6D, 79 in close to equal proportions.

Fin

Okay, it’s fine to look at the data now.

00000000: 0100 0000 0472 656d 7900                 .....remy.

…repeated 24 times.

Now that we’ve identified a single segment of the pattern in the data, we can examine it separately.

In this case, the data is in a very common encoding Type-Length-Value (TLV) in which:

01 is the Type of data (1)

00 00 00 04 is the Length of the data (4)

72 65 6d 79 is the value (remy)

00 Null termination

In a real world scenario we’d now know that the encoding is TLV and that 01 as the Type is a string and have gained a fairly good understanding of the data at hand without ever really needing to look directly at it.

So if you find yourself browsing Archive.org indexes of some Art major’s attempt to create a virtual interactive 3D world using a long deprecated Java plugin in Netscape at 2AM, just remember…

Don’t panic. Look at the shapes.